Copyright 1998-2014 (c) Synthetic Reality Co.
Synthetic Reality: |
| Home Company Store Donations Contact Us |
Games: |
| Well of Souls Arcadia: > Empyrion > synChess > synJet > synPool Warpath 97 Warpath Classic NetSpades MIX Game Server |
Demos: |
| Rocket Club synVertigo synWater synBirds synVista Galaxy Simulator |
Community: |
| Forum About Us FAQ News CASH-CAM Friends |
Money: |
| Donations |
I wanted to write a program with a lot of number-crunching in it to show off what a great investment the computer was and I remembered how multi-body gravitation programs were always considered very challenging back when I was in school.
Well, times change, I guess, cause modern personal computers seem up to very large challenges in that regard.
This program is FREE, not shareware. Just enjoy it.
What Is Galaxy Simulator?
Well, the name is probably a bit of an exaggeration, but basically it starts with a group of stars placed randomly in a 3D volume of space. Then it computes the gravitational attraction between all the stars and moves them all a little. Then it does it again. That's about it, really. I added some extras for fun (like making a movie since it *does* take awhile to compute a large enough number of stars.
And I am considering 2000 to be a large number, which is not really accurate in the 'galaxy' sense, of course. But it's a lot of little dots on your computer monitor.
My 'scientific goal' for the program was to establish that given time, a random placement of stars would turn into a rotating disk (my hypothesis) and it more or less seems to be the case. Since the stars start off at rest (yeah, yeah, I know that would make a nice feature addition to give them initial velocities), they are initially drawn to the center of mass of the universe, and a few encounter each other closely right away and are whipped outwards at high velocity. The rest pass each other on their way through the center, bound out the far side, and eventually slow down and orbit the center. Eventually one plane becomes dominant (mainly by hurling out the stars which aren't in it.) and then one direction of rotation dominates (took me over a week of computation to get to this point, and about half the stars had reached what appeared to be escape velocity in the process.)
Running the Program
Well, just unzip the executable and run it.
| Galaxy Simulator version 1.0 | galaxy.exe |
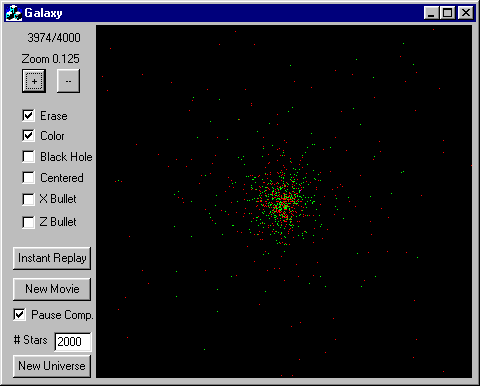
It is a dialog-based MFC app written in VC++ 4.2b Right away it starts animating a universe of 200 stars, which runs in real time on my machine. You can resize the display to your comfort and experiment with the controls along the left. Here is a brief summary of the controls
- Frame Number. The universe begins with frame zero and each new computation of the start positions is another frame. This field shows two numbers. The first is the frame being displayed, the second is the total number of frames computed so far. I record the first 4000 frames in a movie buffer (this tests your memory and disk drive, as well as your computing horsepower). Many of the controls (like the ZOOM buttons) actually rewind your frame playback a little, so you can see over again a second or two of what you just saw.
- Zoom In/Out. These buttons let you zoom in and out. If you click in the galaxy area, you will center the display on the area you clicked on. Any of these operations also rewind the playback buffer a couple seconds. If you are computing a large number of stars, the program will lock up for the time required to complete the computation of the current frame (see the pause computation checkbox) and your clicks on buttons, etc. will be deferred until that frame is computed.
- ERASE. When this is checked, the screen is erased before displaying each frame. This is more like a real Galaxy. Uncheck this box to see lines left behind as stars move (not really lines, you just see the previous positions).
- COLOR. This slows computation a little, but it colors the stars to indicate their absolute velocity changes. Normally stars are all yellow, but when color is turned on they are green while getting faster, and red while slowing down. An orbiting star will generally be green while falling towards the center of its orbit, and red while moving away. It is particularly cool to discover groups of stars in complex orbits around each other. Since the display is not centered on any one star (another possible feature), such orbits look more like figure eights than the ellipses you might otherwise expect.
- BLACK HOLE. This turns on a massive black hole in the center of the galaxy. It is pretty boring if you turn it on too soon as all the stars basically fly through the center and out the far side, never to return (well, not in your lifetime). Turning it on AFTER a few weeks of computation would probably be more interesting.
- CENTERED. This attemps to auto-center the display on the center of mass of the galaxy, but for some reason I can't get my center of mass computations to work right. Or at least, I don't believe the results.
- X Bullet. This fires a massive black hole from the left through the center of the galaxy. It's pretty neat to watch the stars react.
- Z Bullet. Same as X bullet, but the black hole is shot from YOU through the center. It lets you see what is happening better, I think. Basically, all the stars pull towards the center (but the hole is long gone before they get there) and then continue out the far side, creating a conical pattern. This can actually help quickstart the circular/planar nature of your galaxy and who knows, maybe this sort of thing happens in nature all the time?
- INSTANT REPLAY. This starts the movie running from frame zero. New computations are delayed until the moview catches up with the current computation frame. When you are doing a long computation, this is a nice way to see the results of your work.
- PAUSE COMPUTATION. The slow computations with a large number of stars are irritating when you want to browse a bit and watch movies. This checkbox halts computation until you uncheck it again. While paused, you can zoom in and out and click around on interesting areas and have the instant gratification you desire. Don't forget to uncheck it when you are ready to get some more computing under way.
- # STARS. This is where you set the initial number of stars for your galaxy. It won't take effect until you push the NEW UNIVERSE button
- NEW UNIVERS. This starts of a new universe, with a new group of randomly placed stars. Your computation frame starts back at zero and all your computing up to that point is lost.
There is NO WAY to save a movie, or the results of your hard-won computations. The whole point is to enjoy it while it is happening.
The Math
It's all pretty basic physics (all Newtonian, no time dilation is involved). But to make things educational (and to be properly didactic):
- The force of attraction between any two stars is F = (G * M1 * M2)/(R * R) where G is the universal gravitational constant, M1 and M2 are the masses of the two objects in question, and R is the distance between them. For each 'frame' of the computation, I compute the force vector between each possible pair of stars and add them together to come up with a single vector for each star showing the net force applied to it. It is important to do this BEFORE actually moving ANY of the stars.
- It is the doing of this math between all possible pairs of stars which is why this requires lots of computing power in the first place. For N stars, there are N*N computations required. In fact, I take advantage of the fact that for any given pair of stars they each exert the same force on each other (just in opposite directions, each exactly towards the other one), so I only have to do half the total number of computations, or (N * N)/2. The inverse square law would let me simplify additionally by not bothering to compute the contribution of distant objects, but heck, why not? It's more fun this way.
- Some trigonometry is required to break the net force vector down into 3 component parts for the X, Y , and Z coordinate axes. Basically this is done by computing the differences in the XYZ positions of the two stars (which gives you a line segment from the center of one star to the other), scaling it until it is of length 1.0 (by dividing each coordinate by the absolute length of the line - which requires a square root operation, which was one of my goals :-) and then multiplying each scaled coordinate by the total force F to get the 3 components of the force vector Fx Fy and Fz.
- The acceleration of a star is derived from F = M * A (or A = F / M, since we are solving for acceleration). So we take the net force applied to the star (which is a vector, meaning it has both a strength and a direction) and divide it by the mass of that star. The acceleration is another vector, so we have to compute Ax = Fx/M, Ay = Fy/M, and Az = Fz/M to get the amount of acceleration to apply in each coordinate direction.
- The velocity of a star (which remains constant until acted upon by an external force, don't you know) starts out at zero and is influenced in each frame by the net acceleration of that frame. Because I can control the structure of the simulation, I can simplify this to just the acceleration times the elapsed time of the frame. And since I designed the whole thing around certain time units as scaling factors, I can actually just use the acceleration value itself. So the previous velocity vector of the star is modified by the current frame's acceleration, as in Vx = Vx + Ax, but your math teacher would prefer that you saw that as: V = V + (A * deltaT)
- The new position of a star is influenced both by its velocity, and the acceleration it experienced in that frame. The reason the acceleration is in there is basically due to the fact that since the velocity wasn't really constant throughout the frame, and the acceleration helps summarize that. So the official equation for position is P = P + (V * T) + (A * T * T)/2, where T is the elapsed time of the frame. Again, my choice of units allowed the T terms to drop out (by being '1.0' basically), so I only had to compute P + V + (A/2). Of course, this had to be computed separately for each of the three coordinate axes as in Px = Px + Vx + (Ax/2), etc.
- I used double-precision floating point math for all the computations and, sparing any leftover Pentium errors, I don't think I experienced much round-off error. I modeled the stars as point sources (I guess they are more like black holes really) and didn't do any actual collision detection, so I don't claim absolute accuracy. But the lack of relativisitic effects makes this just a toy anyway.
The stars are all unrealistically heavy, just to get things interesting as soon as possible, and as mentioned before, a REAL galaxy has a lot more stuff in it, but 2000 stars puts on a satisfying show. The center of the galaxy becomes an interesting dance of fireflies.
COPYRIGHT
Galaxy Simulator is the property of Synthetic Reality and all rights are reserved. If we can figure out a way to convince people to pay for this, you can be sure we'll give it a try. But for now it is expressly intended to provide a moment of joy for the math geeks in the audience, looking for number-crunching programs to show off their power computers!
Thanks for your feedback in advance!
Dan Samuel
Synthetic Reality Co.